Photo Forensics: In the Shadows
When asked to judge the location of the sun relative to this scene, most people would respond quickly that it is on the right. When asked to localize the sun more precisely, most people would need to think before responding and they would still be inaccurate. (For evidence of this perceptual failure see 1Hany Farid and Mary J. Bravo. Image Forensic Analyses that Elude the Human Visual System. SPIE Symposium on Electronic Imaging, San Jose, CA, 2010., but also test yourself: the answer is below.) The difficulty we have localizing light sources is surprising because the scene contains abundant information for making this judgment. The fact that we cannot easily perceive information that is clearly contained within the image provides an opening for forensic analysis because forgers may be unaware that they have introduced telltale clues that we can easily detect. In this post, we will see how to determine whether the cast shadows in an image are consistent with a single light source. If the shadows are inconsistent in a scene that is clearly illuminated by a single source (e.g., the sun), then we have strong evidence of image tampering.

Let’s start our analysis of this image by considering the central shadow cast by the light post. For every point around the outside of the shadow, there must be a line to the light source that is unobstructed by the lamppost. For every point within the shadow, there must be a line to the light source that passes through the lamppost (the lamppost intercepts the line, causing the point to be in shadow). So, if we draw a line connecting a point on the shadow boundary with its corresponding point on the lamppost, this line will intersect the light. This is true in the 3-D world and it is also true in the 2-D image. (We assume that there is no lens distortion so that a straight line in the world appears as a straight line the image. If lens distortion causes lines to bend, we must reverse the distortion before we can perform this analysis.) This observation lies at the heart of our analysis, and so it is worth emphasizing: just as a point on the lamppost shadow, the corresponding point on the lamppost, and the light source are all constrained to lie on a single 3-D line in the world; the image of a point on the lamppost shadow, the image of the point on the lamppost, and the image of the light source are all constrained to lie on a single 2-D line in the image. This idea is illustrated below, which shows a line that connects a point on the cast shadow to the corresponding point on the lamppost. In the 2-D image, the projection of the light source lies somewhere on this (infinite) line.

Now let's draw more lines connecting corresponding points between objects and shadows. If the scene has a single light source, then these lines must intersect at a point that corresponds to the location of the light. If the light source is not visible in the image, as is typically the case, then this intersection will lie outside the boundary of the image. Depending on where the light is, it may be necessary to extend the lines beyond the image boundary on the left, right, top, or (counter-intuitively) bottom. In rare situations, the intersection may be at infinity (all of the lines are parallel to one another).
The geometric constraint relating the shadow, the object, and the light holds for a light source at any distance, whether it is a nearby desk lamp or the distant sun. This constraint also holds for any surface onto which the shadow is cast regardless of the surface's location and orientation. Consider the shadow from the backward facing street sign on the left. Part of the shadow falls on the face of the building perpendicular to the street. Nonetheless, the line connecting a point on this shadow to a point on the sign will still intersect the light source.
If a forger adds or moves an object in an image, it is possible that he or she will fail to perfectly align all of the corresponding shadows. The geometric constraint described above affords a simple and powerful technique for analyzing the shadows in an image for consistency and plausibility.
Example
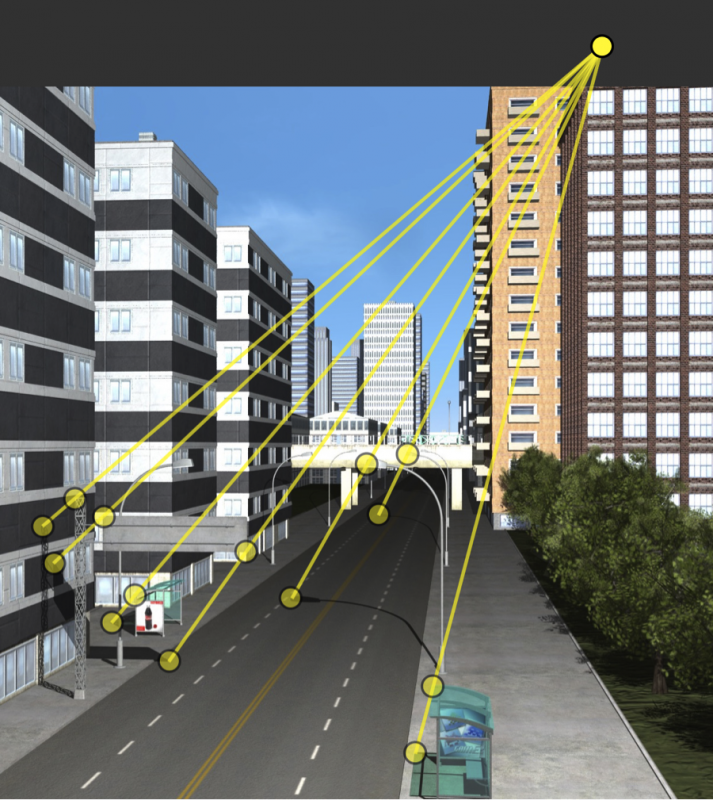
I’ve taken a car from an unrelated scene and digitally inserted it into the city street scene. Few people would find anything amiss with this manipulated scene. Let’s apply our shadow analysis to see if the shadows are in fact consistent with an outdoor scene illuminated by the sun.

Shown below are several shadow-object correspondences from the surrounding scene (yellow) and the car (cyan). As before, the lines generated from the shadows in the surrounding scene intersect at one point. But the lines connecting the car and its shadow do not share this intersection. This inconsistency in light source location is a clear sign of photo tampering.

Caveats
A few words of caution when applying this shadow analysis:
- The accuracy and precision of this analysis depend on the accuracy and the precision of the lines drawn between corresponding points on objects and shadows. Care should be taken to precisely select corresponding features. (If it is difficult to determine exact correspondences, then a related technique can be used, see 2Eric Kee, James O’Brien, and Hany Farid. Exposing Photo Manipulation with Inconsistent Shadows. ACM Transactions on Graphics, 32(4):28:1–12, 2013.);
- When analyzing outdoor scenes it is reasonable to assume, as we have, that the scene is illuminated by a single light source (the sun). Indoor scenes, however, may contain multiple light sources that selectively illuminate one part of the scene and not another. In this case, the analysis can only be applied to the regions of the scene that clearly share a single light source;
- The analysis may localize the light source in a counter-intuitive location, such as below the frame of the image. This is not evidence of a forgery: When the light is behind the camera, its projection will be in the lower half of the image.
Summary
In a 3-D scene, all lines connecting points on a cast shadow and their corresponding points on an object intersect at the light source. In the 2-D image, these lines intersect at the projection of the light source. The projection of the light source may be visible in the image or it may fall outside of the image (to the left, right, above, or below). This constraint holds regardless of the distance and location of the light source and regardless of the geometry of the surface onto which the shadows are cast. Cast shadows are consistent with a single light source if the lines connecting corresponding points on objects and their shadows all intersect at a single point.
Further Reading
Eric Kee, James O’Brien, and Hany Farid. Exposing Photo Manipulation from Shading and Shadows. ACM Transactions on Graphics, 33(5):165:1–165:21, 2014.
Portions of this entry are adapted from my upcoming book, Photo Forensics (MIT Press).